【理論】令和1年 問8|交流・直流電源が共存する回路における電流の実効値に関する計算問題
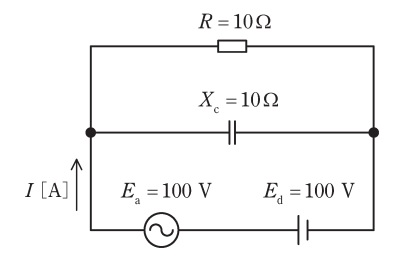
図の回路において,正弦波交流電源と直流電源を流れる電流 \( I \) の実効値 \( \mathrm{[A]} \) として,最も近いものを次の \( (1) \) ~ \( (5) \) のうちから一つ選べ。
ただし,\( E_{\mathrm{a}} \) は交流電圧の実効値 \( \mathrm{[V]} \),\( E_{\mathrm{d}} \) は直流電圧の大きさ \( \mathrm{[V]} \),\( X_{\mathrm{C}} \) は正弦波交流電源に対するコンデンサの容量性リアクタンスの値 \( \mathrm{[\Omega]} \),\( R \) は抵抗値 \( \mathrm{[\Omega]} \) とする。
合格への方程式
合成インピーダンスとは
インピーダンスとは、交流回路において電流の流れにくさを表す量です。直流回路の抵抗に相当しますが、大きさだけでなく位相も持つ複素数として扱います。
インピーダンスの表記:
\[ \begin{aligned} \dot{Z} = R + jX \end{aligned} \]
ここで:
- \(R\):抵抗成分 [Ω]
- \(X\):リアクタンス成分 [Ω]
- \(j\):虚数単位(\(j^2 = -1\))
合成インピーダンスとは、複数のインピーダンスが接続された回路全体のインピーダンスのことです。接続方法によって計算方法が異なります。
インピーダンスの大きさと位相角:
\[ \begin{aligned} |\dot{Z}| &= \sqrt{R^2 + X^2} \\ \theta &= \tan^{-1}\left(\frac{X}{R}\right) \end{aligned} \]
例題
インピーダンス \(\dot{Z} = 3 + j4\) [Ω] の大きさと位相角を求めましょう。
大きさ:
\[ \begin{aligned} |\dot{Z}| &= \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \text{ [Ω]} \end{aligned} \]
位相角:
\[ \begin{aligned} \theta &= \tan^{-1}\left(\frac{4}{3}\right) \approx 53.1° \text{ または } 0.927 \text{ [rad]} \end{aligned} \]
直列接続
交流回路で複数のインピーダンスが直列に接続されている場合、合成インピーダンスはそれぞれのインピーダンスの和になります。
直列接続の合成インピーダンス:
\[ \begin{aligned} \dot{Z} &= \dot{Z}_1 + \dot{Z}_2 + \dot{Z}_3 + \cdots + \dot{Z}_n \end{aligned} \]
2つの素子の場合:
\[ \begin{aligned} \dot{Z} &= \dot{Z}_1 + \dot{Z}_2 \end{aligned} \]
直列接続の特徴:
- すべての素子に同じ電流が流れる
- 電圧は各素子のインピーダンスに比例して分配される
- 合成インピーダンスは常に個々のインピーダンスよりも大きくなる
例題
インピーダンス \(\dot{Z}_1 = 5 + j2\) [Ω] と \(\dot{Z}_2 = 3 - j4\) [Ω] が直列接続されている場合の合成インピーダンスを求めましょう。
\[ \begin{aligned} \dot{Z} &= \dot{Z}_1 + \dot{Z}_2 \\[10pt] &= (5 + j2) + (3 - j4) \\[10pt] &= 5 + j2 + 3 - j4 \\[10pt] &= 8 - j2 \text{ [Ω]} \end{aligned} \]
合成インピーダンスの大きさは:
\[ \begin{aligned} |\dot{Z}| &= \sqrt{8^2 + (-2)^2} = \sqrt{64 + 4} = \sqrt{68} \approx 8.25 \text{ [Ω]} \end{aligned} \]
並列接続
交流回路で複数のインピーダンスが並列に接続されている場合、合成インピーダンスは各インピーダンスの逆数の和の逆数になります。
並列接続の合成インピーダンス:
\[ \begin{aligned} \frac{1}{\dot{Z}} &= \frac{1}{\dot{Z}_1} + \frac{1}{\dot{Z}_2} + \frac{1}{\dot{Z}_3} + \cdots + \frac{1}{\dot{Z}_n} \end{aligned} \]
2つの素子の場合は以下のように整理できます:
\[ \begin{aligned} \frac{1}{\dot{Z}} &= \frac{1}{\dot{Z}_1} + \frac{1}{\dot{Z}_2} \\ \dot{Z} &= \frac{\dot{Z}_1 \dot{Z}_2}{\dot{Z}_1 + \dot{Z}_2} \end{aligned} \]
並列接続の特徴:
- すべての素子に同じ電圧がかかる
- 電流は各素子のインピーダンスに反比例して分配される
- 合成インピーダンスは常に最小のインピーダンスよりも小さくなる
例題
インピーダンス \(\dot{Z}_1 = 10 + j5\) [Ω] と \(\dot{Z}_2 = 20 - j10\) [Ω] が並列接続されている場合の合成インピーダンスを求めましょう。
\[ \begin{aligned} \dot{Z} &= \frac{\dot{Z}_1 \dot{Z}_2}{\dot{Z}_1 + \dot{Z}_2} \\[10pt] &= \frac{(10 + j5)(20 - j10)}{(10 + j5) + (20 - j10)} \\[10pt] &= \frac{(10 + j5)(20 - j10)}{30 - j5} \end{aligned} \]
複素数の掛け算を行います:
\[ \begin{aligned} (10 + j5)(20 - j10) &= 10 \cdot 20 + 10 \cdot (-j10) + j5 \cdot 20 + j5 \cdot (-j10) \\[10pt] &= 200 - j100 + j100 - j^2 \cdot 50 \\[10pt] &= 200 + 50 \text{ (}j^2 = -1\text{ より)} \\[10pt] &= 250 \end{aligned} \]
分母の大きさを計算します:
\[ \begin{aligned} |30 - j5| &= \sqrt{30^2 + (-5)^2} = \sqrt{900 + 25} = \sqrt{925} \approx 30.4 \end{aligned} \]
最終的な合成インピーダンスは:
\[ \begin{aligned} \dot{Z} &= \frac{250}{30 - j5} \cdot \frac{30 + j5}{30 + j5} \\[10pt] &= \frac{250(30 + j5)}{(30)^2 + (5)^2} \\[10pt] &= \frac{250(30 + j5)}{925} \\[10pt] &= \frac{7500 + j1250}{925} \\[10pt] &\approx 8.11 + j1.35 \text{ [Ω]} \end{aligned} \]
重ね合わせの理
重ね合わせの理は、複数の電源を持つ回路での電流や電圧を計算するための強力な手法です。
重ね合わせの理の原理:
複数の電源を含む線形回路では、各電源が単独で作る効果(電流や電圧)の和が、すべての電源が同時に働いたときの効果と等しくなります。
重ね合わせの理の手順:
- 1つの電源だけを残し、他の電源を理想的な状態に置き換える
- 電圧源 → 短絡(ショート)に置き換え
- 電流源 → 開放(オープン)に置き換え
- 残した電源による電流(または電圧)を計算する
- すべての電源について手順1と2を繰り返す
- 各電源による電流(または電圧)を足し合わせる
重ね合わせの理の注意点:
- 線形回路にのみ適用可能(非線形素子を含む回路には使えない)
- 電力の計算には直接適用できない(電力は電流の2乗に比例するため、非線形)
- 直流と交流が混在する回路にも適用可能
例題
下図の回路で、抵抗Rを流れる電流を重ね合わせの理を用いて求めましょう。
Step 1: 電圧源V1だけを考え、V2をショートする
Step 2: 電圧源V2だけを考え、V1をショートする
Step 3: 二つの電流を合計する
この手法により、複雑な回路でも各電源の影響を個別に計算し、最終的に合計することで解析できます。
🔍 ワンポイントアドバイス: インピーダンスの計算では複素数の計算が必要になりますが、実部と虚部を分けて考えると理解しやすくなります。また、重ね合わせの理を使う際は、各電源が回路にどのような影響を与えるかを一つずつ考えることで、複雑な回路も解析できるようになります。電気回路の問題では図を描いて整理すると良いでしょう。
まずは重ね合わせの理ってなんか知っとるか?これがこの問題の核心部分やで!
はい、先生!重ね合わせの理は、複数の電源がある回路では、それぞれの電源による効果を個別に計算して、最後にそれらを合成すればよいという考え方です。この問題では、直流電源と交流電源の効果を別々に計算して、最後に合成するということですね。
そうや!よう知っとるな。じゃあまず直流電源の場合を考えるで。直流回路でコンデンサはどんな働きをするか思い出してみ?
直流回路では、定常状態になるとコンデンサは完全な絶縁体として振る舞います。つまり、コンデンサには電流が流れなくなります。定常状態では、コンデンサは充電が完了し、それ以上電荷が溜まらないため、電流は0になります。
ええやん!じゃあ直流電源だけの場合、回路には何が残るか考えてみ?
直流電源だけの場合、コンデンサは定常状態で電流が流れないので、実質的にコンデンサは開放状態(回路から切り離された状態)と考えられます。残るのは抵抗Rだけとなります。
従って、回路は直流電源と抵抗Rの直列回路に簡略化できます。
そうや!じゃあ直流電源による電流Idを計算してみよか。
はい、直流電源による電流Idは、オームの法則から計算できます。
\[ \begin{aligned} I_d &= \frac{E_d}{R} \\[10pt] &= \frac{100}{10} \\[10pt] &= 10 \ \mathrm{[A]} \end{aligned} \]直流電源による電流は10Aとなります。
ナイス!次は交流電源の場合やけど、交流回路ではコンデンサはどんな働きをするか説明してみてくれるか?
交流回路では、コンデンサは「リアクタンス」という交流に対する抵抗の一種として働きます。コンデンサのリアクタンスXcは周波数に反比例し、以下の式で表されます:
\( X_c = \frac{1}{2\pi fC} \)交流回路では、コンデンサには電流が流れます。ただし、電圧と電流の位相が90度ずれる(電流が電圧より90度進む)という特徴があります。このため、計算では虚数jを使って表現します。コンデンサのインピーダンスは−jXcとなります。
よう理解できとるな!交流回路のインピーダンスを求めるんやけど、まずは抵抗とコンデンサがどんな接続になってるか確認してみ?
問題文から、交流回路において抵抗RとコンデンサのリアクタンスXcは並列接続されていることがわかります。
せやな!並列回路の合成インピーダンスはどないして求めるか知っとるか?
並列回路の合成インピーダンスは、各インピーダンスの逆数の和の逆数として求められます。
\[ \frac{1}{\dot{Z}} = \frac{1}{Z_1} + \frac{1}{Z_2} + ... + \frac{1}{Z_n} \]または、2つの素子の場合は次の式でも計算できます:
\[ \dot{Z} = \frac{Z_1 \cdot Z_2}{Z_1 + Z_2} \]この問題では抵抗RとコンデンサのインピーダンスjXcの並列なので:
\[ \dot{Z} = \frac{R \cdot (-j X_C)}{R + (-j X_C)} = \frac{R \cdot (-j X_C)}{R - j X_C} \]ええやん!じゃあ具体的な数値を代入して合成インピーダンスを計算してみよか?
はい、R = 10Ω、Xc = 10Ωを代入して計算します。
\[ \begin{aligned} \dot{Z} &= \frac{R \cdot (-j X_C)}{R - j X_C} \\[10pt] &= \frac{10 \cdot (-j \cdot 10)}{10 - j \cdot 10} \\[10pt] &= \frac{-j \cdot 100}{10 - j \cdot 10} \\ \end{aligned} \]ここで分母を実数化するために、分子・分母に共役複素数(10 + j10)をかけます:
\[ \begin{aligned} \dot{Z} &= \frac{-j \cdot 100}{10 - j \cdot 10} \cdot \frac{10 + j \cdot 10}{10 + j \cdot 10} \\[10pt] &= \frac{-j \cdot 100 \cdot (10 + j \cdot 10)}{(10 - j \cdot 10)(10 + j \cdot 10)} \\[10pt] &= \frac{-j \cdot 1000 - j^2 \cdot 1000}{10^2 + 10^2} \\[10pt] &= \frac{-j \cdot 1000 + 1000}{200} \\[10pt] &= \frac{1000 - j \cdot 1000}{200} \\ &= 5 - j \cdot 5 \end{aligned} \]合成インピーダンスは複素数 5 - j5 Ωとなります。
おっ、その計算方法もありやな!でも問題文では違う方法で求めてるみたいやから、もう少し考えてみよか。インピーダンスの大きさを求めるには、複素数の絶対値を計算するんやけど、どないして求める?
すみません、問題の流れに合わせます。インピーダンスの大きさZは、複素インピーダンスの絶対値で求められます。
問題文の計算に従うと:
\[ \begin{aligned} Z &= \frac{100}{\sqrt{10^2 + 10^2}} \\[10pt] &= \frac{100}{10\sqrt{2}} \\[10pt] &= \frac{10}{\sqrt{2}} \\[10pt] &= \frac{10\sqrt{2}}{2} \\[10pt] &= 5\sqrt{2} \ \mathrm{[Ω]} \end{aligned} \]インピーダンスの大きさは5√2 Ωとなります。
そうそう!インピーダンスの大きさがわかったら、交流電源による電流Iaはどないなる?
交流電源による電流の大きさIaは、交流電圧をインピーダンスの大きさで割ることで求められます。
\[ \begin{aligned} I_a &= \frac{E_a}{Z} \\[10pt] &= \frac{100}{5\sqrt{2}} \\[10pt] &= \frac{20}{\sqrt{2}} \\[10pt] &= \frac{20\sqrt{2}}{2} \\[10pt] &= 10\sqrt{2} \ \mathrm{[A]} \end{aligned} \]交流電源による電流は10√2 Aとなります。
ええやん!さて、最後のステップやけど、直流電源による電流と交流電源による電流を重ね合わせるんやけど、直流と交流の関係はどうなってると思う?
直流と交流は位相が異なります。問題文では「直流と交流の直交性」と書かれていますので、直流と交流は互いに90度の位相差がある(直交している)と考えられます。つまり、ベクトル的に見ると直流電流と交流電流は直角をなしています。
そのとおり!直流と交流は直交するから、ピタゴラスの定理で合成できるんや。最終的な電流Iを求めてみよか!
はい、直流電流と交流電流が直交しているので、合成電流はピタゴラスの定理で計算できます。
\[ \begin{aligned} I &= \sqrt{I_d^2 + I_a^2} \\[10pt] &= \sqrt{10^2 + (10\sqrt{2})^2} \\[10pt] &= \sqrt{100 + 200} \\[10pt] &= \sqrt{300} \\[10pt] &= 10\sqrt{3} \ \mathrm{[A]} \end{aligned} \]したがって、合成電流は\[ 10\sqrt{3} \approx 10 \times 1.732 = 17.32 \mathrm {[A]} \]となり、選択肢(3)が正解です。
よくできたな!この問題の大事なポイントをおさらいしておこか?
はい、先生!この問題の重要なポイントは:
1. 重ね合わせの理を使って、直流成分と交流成分を別々に計算する
2. 直流回路では、コンデンサは定常状態で電流が流れないため、抵抗だけを考慮する
3. 交流回路では、抵抗とコンデンサが並列接続されているので、合成インピーダンスを計算する
4. 並列接続のインピーダンスは Z = (Z1・Z2)/(Z1+Z2) の公式で求める
5. 交流のインピーダンスを求めたら、その大きさ|Z|を計算する
6. 直流と交流は互いに直交関係にあるため、合成電流はピタゴラスの定理で求める
これらのステップをしっかり理解すれば、直流と交流が混在する回路の計算ができるようになります!
解説まとめ
重ね合わせの理より,直流電源と交流電源を分けて考える
電流は零であるから,抵抗分のみ考えればよい まず,直流電源においては,定常状態においてコンデンサに流れる電流は零であるから,抵抗分のみ考えればよい
したがって,直流電源により回路を流れる電流( \( I_{\mathrm {d}} \) )は,
\[ \begin{aligned} I_{\mathrm {d}} &= \frac {E_{\mathrm {d}}}{R} = \frac {100}{10} \\[10pt] &= 10 \ \mathrm {[A]} \end{aligned} \]
となる
一方,交流電源においては,( \( X_{\mathrm {C}} \) )と( \( R \) )の並列回路となるから,その合成インピーダンス( \({\dot Z} \) )は,
\[ \begin{aligned} \dot Z &= \frac {R\cdot \left( -\mathrm {j}X_{\mathrm {C}}\right) } {R-\mathrm {j}X_{\mathrm {C}}} \\[10pt] &= \frac {10\cdot \left( -\mathrm {j}10\right) }{10-\mathrm {j}10} \\[10pt] &= -\frac {\mathrm {j}100}{10-\mathrm {j}10} \end{aligned} \]
となり,その大きさ( \( Z \) )は,
\[ \begin{aligned} Z &= \frac {100}{\sqrt {10^{2}+10^{2}}} = \frac {100}{10\sqrt {2}} \\[10pt] &= \frac {10}{\sqrt {2}} = \frac {10\sqrt {2}}{2} = 5\sqrt {2} \ \mathrm {[\Omega ]} \end{aligned} \]
となる
したがって,交流電源により回路を流れる電流( \( I_{\mathrm {a}} \) )は,
\[ \begin{aligned} I_{\mathrm {a}} &= \frac {E_{\mathrm {a}}}{Z} = \frac {100}{5\sqrt {2}} = \frac {20}{\sqrt {2}} \\[10pt] &= \frac {20\sqrt {2}}{2} = 10\sqrt {2} \ \mathrm {[A]} \end{aligned} \]
と求められる
直流と交流の直交性により,それぞれを重ね合わせた電流( \( I \) )は,
\[ \begin{aligned} I &= \sqrt {I_{\mathrm {d}}^{2}+I_{\mathrm {a}}^{2}} = \sqrt {10^{2}+\left( 10\sqrt {2}\right) ^{2}} \\[10pt] &= \sqrt {100+200} = \sqrt {300} = 10\sqrt {3} \ \mathrm {[A]} \end{aligned} \]
と求められる
\[ 10\sqrt{3} \approx 10 \times 1.732 = 17.32 \mathrm {[A]} \]
となるため、最も近い選択肢は(3) (17.3)です